- Publié le 10 janv. 2023
- Mis à jour le 15 déc. 2025
- 21 min
Traitement numérique du signal - Définition, fonctionnement et bénéfices

Le monde réel est analogique ! Pourquoi chaque machine ou instrument qui nous entoure est-il à la maison ou au bureau de plus en plus décrit comme "numérique" ? Pour répondre à cette question, il faut commencer par expliquer ce que nous entendons par le mot "analogique" .
Choisir un traitement numérique du signal plutôt qu'un traitement analogique
Toutes les choses mesurables dans la vie varient continuellement en amplitude (taille) avec le temps : la température extérieure, la vitesse d'une voiture ou même la lumière du jour. Nous pouvons convertir une température variable en tension électrique variable à l'aide d'un capteur. Nous obtenons donc un analogue électrique de l'effet d'origine. La tension varie en fonction de la température. Une fois que nous avons ce signal analogique, nous pouvons le traiter à l'aide d'autres composants électroniques et afficher un relevé de température sur un simple instrument à aiguille. Le point important à retenir est que les paramètres naturels varient en permanence, et non en pas discrets ; même les appareils qui semblent fonctionner de manière discrète ou numérique peuvent être trompeurs.
Mesurer le monde
Si nous devons mesurer une longueur, nous pouvons utiliser une règle ou un mètre à ruban. Mais que se passe-t-il si nous voulons qu'une machine prenne la mesure ? Nous souhaiterions peut-être que la mesure s'affiche en différentes unités en fonction de la position d'un commutateur, ou que la machine utilise les informations mesurées et réalise une action appropriée. Nous avons besoin d'un système électrique ou électronique qui convertisse tout ce que nous essayons de mesurer en signal électrique, peut-être en effectuant un traitement du signal avant d'afficher ou de transmettre le résultat.
En résumé, les composants dont nous avons besoin sont :
- un ou plusieurs capteur(s), pour convertir le paramètre mesuré en signal électrique
- un système de traitement des signaux, analogique et/ou numérique
- et peut-être, un retour d'information pour la commande en "boucle fermée" ou automatique.

Systèmes analogiques simples
Un système de mesure-affichage à unité unique ne nécessite aucun traitement. Par exemple, le thermomètre au mercure, le baromètre au mercure et l'ampèremètre à bobine mobile. Veuillez noter que ce sont tous des systèmes "analogiques", qui convertissent directement un paramètre en affichage visible.
Le système de mesure-affichage en deux parties nécessite généralement peu ou pas de traitement et, avant que les voitures ne deviennent "numériques", des exemples de mesure-affichage analogique peuvent être trouvés dans les jauges de carburant et l'instrumentation de température de l'eau. Dans les deux cas, nous avons un capteur séparé qui convertit le paramètre en signal électrique, dans ces cas le courant, et un affichage. Cet affichage utilise ure méthode à fil chaud pour convertir la valeur de courant en position d'aiguille.
Les systèmes de mesure-traitement-affichage sont électroniquement plus complexes que les exemples ci-dessus car des circuits de conditionnement de signal sont placés entre le capteur et le dispositif d'affichage/sortie. Traditionnellement, il s'agit de circuits "analogiques" composés de transistors, de résistances, de condensateurs et plus récemment de circuits intégrés ou de "puces". Veuillez noter que toutes les puces ne sont pas numériques. Un "traitement du signal" courant est l'élimination du bruit électrique haute fréquence d'un moteur électrique à proximité. Dans ce cas, le circuit serait probablement un filtre passe-bas.
Quel est le problème du traitement analogique ?
Les systèmes présentés ci-dessus sont décrits comme "traditionnels" car ils représentent une époque en termes de techniques électriques/électroniques et de mesure qui remonte à plusieurs siècles. Ils avaient l'avantage d'être fiables et économiques à fabriquer (en grandes quantités). Le traitement du signal analogique était réduit au minimum car les composants électroniques étaient coûteux, peu fiables et nécessitaient des ingénieurs de conception qualifiés pour les faire fonctionner. Examinons cela plus en détail.
Les tolérances des composants constituent un véritable casse-tête pour le concepteur de matériel analogique. Des valeurs très spécifiques de résistances ou de condensateurs peuvent être nécessaires pour réaliser une spécification particulière, mais seules certaines valeurs couramment utilisées sont fabriquées. Cela peut entrainer le recours à des composants variables au coût bien plus élevé, et la nécessité de faire des réglages après la production.
Aujourd'hui, le vieillissement des composants est moins problématique grâce aux nouveaux matériaux, mais il peut encore être important. Par exemple, une résistance peut avoir une certaine valeur de résistance en quittant l'usine, mais elle peut avoir suffisamment varié des années plus tard pour que le circuit sorte de ses spécifications d'origine ou défaille complètement.
Le bruit électrique ou les interférences induites dans le circuit analogique peuvent parfois être éliminés par des circuits supplémentaires, si elles peuvent être distinguées du signal souhaité. Le plus souvent, l'électronique ne peut pas faire la différence entre le bruit et le signal. Prenez par exemple les vieux tourne-disques : il est impossible d'éliminer le "cratch" de l'aiguille, le "grondement" du plateau tournant, les clics, les claquements et les sifflements sans supprimer des morceaux de musique. Votre cerveau peut tout trier, mais même le système de traitement analogique le plus sophistiqué en est incapable. Le mieux que vous puissiez espérer est de réduire le bruit global à un niveau acceptable.
Une conception matérielle complexe est nécessaire, même pour les tâches de traitement simples. Même si vous souhaitez seulement intégrer un filtre passe-bas, c'est-à-dire supprimer toutes les fréquences au-dessus d'une certaine valeur du signal, vous ne trouverez pas la tâche facile. En fonction des spécifications de performances précises, il existe un grand nombre de techniques possibles, chacune nécessitant un nombre encore plus grands de circuits possibles. Les problèmes de tolérance s'ajoutent et, si cela ne suffisait pas, la configuration et la conception de la carte de circuit imprimé (PCB) sur laquelle elle est conçue peuvent ajouter des effets de capacité "vagabonde", ce qui entraîne une instabilité dans une conception à haute fréquence. Les compromis de conception sont inévitables.
Les difficultés en termes de débogage, de modification ou de mise à niveau d'une conception matérielle analogique rendent le produit coûteux au départ, avec beaucoup d'efforts nécessaire par la suite. Les erreurs de conception du circuit entraînent le remplacement physique des composants et la refabrication des circuits imprimés. Les mises à niveau ultérieures impliquent souvent des modifications physiques similaires, ce qui ne vaut généralement pas la peine, et l'ensemble du système est conçu à nouveau de A à Z.
Le numérique à la rescousse
Heureusement, le salut est à portée de main avec l'invention de l'ordinateur et du traitement numérique des signaux ou en temps discret. Dans les années 1920, Harry Nyquist, ingénieur télégraphique, a fondé ce que nous appelons désormais le traitement numérique du signal, même s'il s'est lui-même inspiré de travaux beaucoup plus anciens par d'autres. Pour tirer parti des avantages du traitement numérique du signal, nous devons passer du traitement en temps continu que nous utilisions jusqu'alors, au traitement à temps discret.
Qu'entend-on par "temps discret" ? Nyquist et d'autres ont démontré mathématiquement qu'il était possible de travailler sur des échantillons d'un signal pris à intervalles réguliers et continuer à obtenir un résultat satisfaisant. Cela semble bizarre, mais c'est vrai : vous pouvez prendre un échantillon de forme d'onde ou de signal continu, puis reconstruire le signal continu d'origine exactement à partir de ces échantillons. Et mieux encore ; la règle qui régit cet échantillonnage, appelée théorème d'échantillonnage de Nyquist-Shannon, est très simple, mais sans elle, il n'y aurait pas de traitement numérique du signal. Il n'est pas nécessaire de comprendre la démonstration mathématique complexe derrière cette équation très simple pour l'utiliser :
fs>2B, dans laquelle fs est la fréquence d'échantillonnage et B la largeur de bande du signal échantillonné.
Ainsi, si vous avez, mettons, un signal audio avec une limite de fréquence maximale de 15 kHz, vous aurez alors besoin d'une fréquence d'échantillonnage de plus de 30 000 échantillons/seconde. Naturellement, il existe une ou deux "limites" dont je parlerai plus tard, mais de manière générale, si vous échantillonnez le signal à cette fréquence, il est possible de récupérer exactement la forme d'onde analogique d'origine.
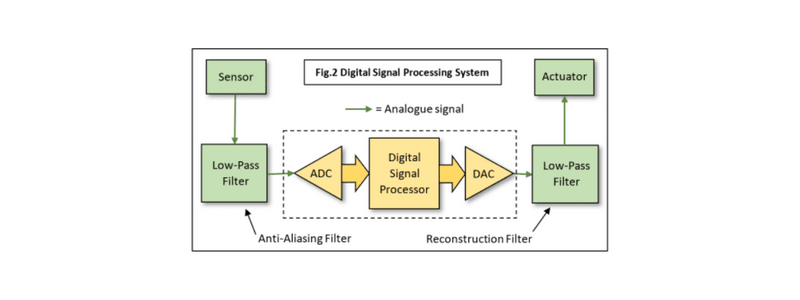
Tout ce dont nous avons besoin est appelé un convertisseur analogique-numérique (ADC), qui prend une "capture" de la tension du signal à intervalles réguliers, convertit ce niveau de tension en un nombre numérique binaire et le transmet à un ordinateur numérique qui, bien sûr, adore les nombres binaires. (Fig.2).
Un dispositif plus simple, appelé un convertisseur numérique-analogique (DAC), reçoit les nombres de l'ordinateur et les transforme en échantillons de tension. Les implications sont énormes...
Les tolérances des composants et d'autres problèmes de conception matérielle disparaissent presque entièrement, la plupart des circuits de traitement analogique étant remplacés par des algorithmes logiciels exécutés sur la puce de traitement numérique. Le débogage et la mise à niveau sont ainsi beaucoup plus simples et moins chers car les systèmes de traitement numérique sont beaucoup plus faciles à reprogrammer que les systèmes analogiques à reconstruire.
Le vieillissement n'est désormais qu'un problème à long terme, et il a également une caractéristique numérique : le système fonctionne ou non selon les spécifications. En supposant que le logiciel a été complètement débogué, la fonction de traitement ne changera pas avec le temps, sauf si elle est "piratée". La sécurité du micrologiciel intégré est désormais un véritable défi, les systèmes d'acquisition de données connectés à Internet devenant de plus en plus courants.
Les problèmes de bruit sont réduits. Les CD audio n'ont plus les sifflements ni les cratch des cassettes analogiques et des disques vinyles, car les sons échantillonnés sont stockés sous forme de données numériques et sont lus sans contact physique avec le disque.
Considérations pratiques
La conception d'une application pratique basée sur le traitement numérique du signal n'est évidemment pas si simple.
- Les calculs supposent une impulsion d'échantillonnage de largeur zéro appelée fonction Dirac Delta. Malheureusement, elle n'existe qu'en théorie, et les impulsions réelles de largeur finie entraînent une distorsion de fréquence prévisible. Mais il existe des solutions
- Le filtre passe-bas théorique et parfait, appelé "mur de brique", nécessaire pour s'assurer que le signal ne contient aucune fréquence supérieure à la moitié de la fréquence d'échantillonnage, est également impossible à réaliser. Nous pouvons également contourner ce problème. Veuillez noter que ce filtre analogique est nécessaire avant l'ADC (anticrénelage) et après le DAC ( reconstruction).
- L'ADC convertit le signal en niveaux discrets ; par exemple, un ADC 8 bits a une résolution de 256 niveaux. Cela introduit un bruit de quantification qui peut être réduit en augmentant la résolution de conversion à l'aide d'un ADC 12, 16 ou même 24 bits. Toutefois, de nombreuses applications fonctionnent parfaitement avec 8 bits. Voir la Fig.2.
Choisir un convertisseur analogique-numérique
Se procurer les caractéristiques techniques
Avant de sélectionner un ADC, le concepteur doit disposer d'un certain nombre de données numériques :
- La composante de fréquence maximale du signal analogique.
- La plage dynamique du signal analogique (rapport entre le niveau du signal d'entrée maximal et minimal).
- Le rapport signal/bruit requis du signal numérisé.
Choisir la fréquence d'échantillonnage
La fréquence d'échantillonnage est définie en fonction du critère de Nyquist qui établit qu'elle doit être plus de deux fois supérieure à la composante de fréquence maximale présente dans le signal analogique. Cela garantit une reproduction précise, mais une fréquence beaucoup plus élevée permettra de faciliter la conception d'un circuit essentiel qui se trouve en amont de l'ADC : le filtre anticrénelage.
Considérations de conception pour le filtre anticrénelage
Les tracés de fréquence dans la Fig.1 (ci-dessous) fournissent une représentation graphique du crénelage. Dans cet exemple, nous allons échantillonner un signal de bande de base qui a une composante de fréquence maximale fmax (la bande en vert) à l'aide d'une fréquence d'échantillonnage fS. Le tracé à gauche montre toutes les nouvelles fréquences présentes dans le signal échantillonné non-crénelé. Notez que nous avons maintenant de nouvelles bandes de fréquences (en bleu), chacune d'une largeur de 2 x fmax et centrée sur la fréquence d'échantillonnage fS et ses harmoniques. Il s'agit d'un signal échantillonné correctement parce que fS > 2 x fmax. En revanche le tracé à droite montre un crénelage important où les diverses bandes se chevauchent, ce qui conduit à la production de fréquences erronées dans la bande de base verte.
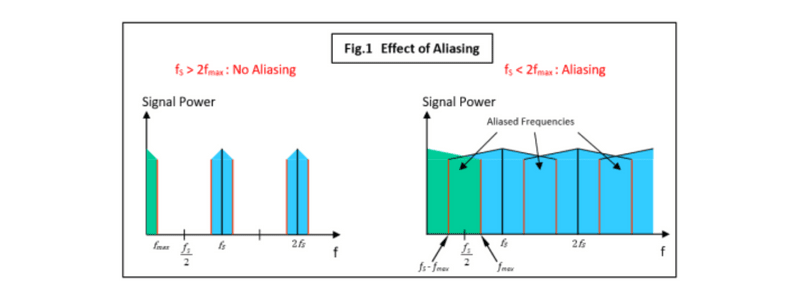
Ne vous inquiétez pas de toutes ces informations créées par le processus d'échantillonnage qui semblent redondantes : les copies de la bande de base enroulée autour de la fréquence d'échantillonnage et de ses harmoniques. Tant qu'aucun chevauchement ne se produit (crénelage), le signal de bande de base analogique d'origine peut être reconstruit exactement. L'image en haut est une représentation graphique d'une simple onde cosinus échantillonnée à une fréquence élevée. Chacune de ces lignes verticales représente la valeur échantillonnée à cet instant, c'est-à-dire la valeur convertie en un nombre numérique par l'ADC et stockée dans la mémoire de l'ordinateur. Comme une onde cosinus n'a qu'une composante de fréquence, le tracé de fréquence qui résulte de l'échantillonnage ressemble à la Fig.1, mais avec seulement les lignes rouges et noires. Notez que, grâce à l'impulsion d'échantillonnage "zéro largeur", les harmoniques de la fréquence d'échantillonnage s'étendent à l'infini. En théorie.
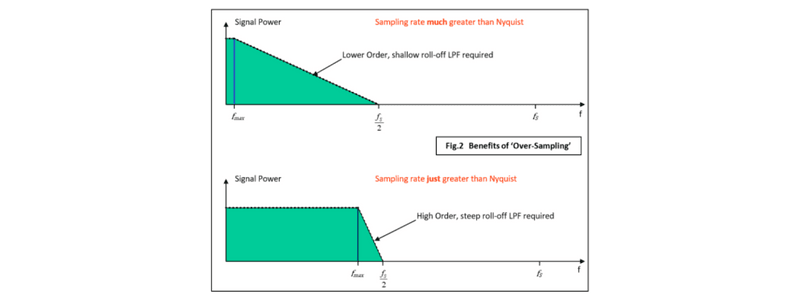
Le problème pratique est que peu de signaux "bruts" ont une fmax nette. Afin d'éviter la production de composants crénelés, un filtre anticrénelage passe-bas doit être placé dans le circuit avant l'ADC. La Fig.2 (ci-dessous) montre le lien entre le taux d'échantillonnage et l'ordre (coupure) du filtre passe-bas. Le concepteur peut très largement suréchantillonner, puis utiliser un simple filtre passe-bas ou sélectionner une fréquence inférieure et ensuite être confronté à la nécessité d'un type multi-pôles complexe.
Cependant, la capacité de l'appareil DSP à traiter l'algorithme entre des échantillons consécutifs doit être prise en compte avant de définir la fréquence d'échantillonnage. On peut éviter beaucoup d'ennuis par la suite si le programme est testé et chronométré sur un système de développement approprié avant de fixer la fréquence d'échantillonnage et de concevoir le filtre.
Un filtre anticrénelage pratique
Un choix commun de filtre analogique est le Sallen-Key (Fig.3, ci-dessous). Ce circuit est conçu pour un filtre Butterworth à 2 pôles (plat maximal dans la bande passante) avec une coupure de 12 dB/octave. Il est probable qu'un filtre à 4 ou 6 pôles soit nécessaire pour réaliser la coupure nécessaire et heureusement, les circuits Sallen-Key peuvent être montés en cascade.
Si R1 = R2 = R et C1 = C2 = C, alors la fréquence de coupure est 1/2pRC Hz. Un gain utile peut être ajouté, donné par K = 1 + (R3/R4).
ADC (nombre de bits/échantillon)
Quelle plage dynamique est nécessaire ? La plage dynamique (DR) est le rapport de la plus petite et de la plus grande amplitude de signal qui sera résolu. En d'autres termes :
- DR = Vmax/Vmin = 2n ou en décibels : DR = 6,02n dB n où n = nombre de bits ADC. Vous pouvez maintenant travailler sur le rapport signal/bruit de quantification (SNR) associé à un nombre de bits en particulier.
- Pour un ADC idéal : SNR = DR + 1,76 dB
- Pour les pires conditions, ½ LSB d'erreur de linéarité ADC : SNR = DR - 4,24 dB
Notez que cette figure SNR (celle ci-dessous) suppose que l'entrée analogique est silencieuse.
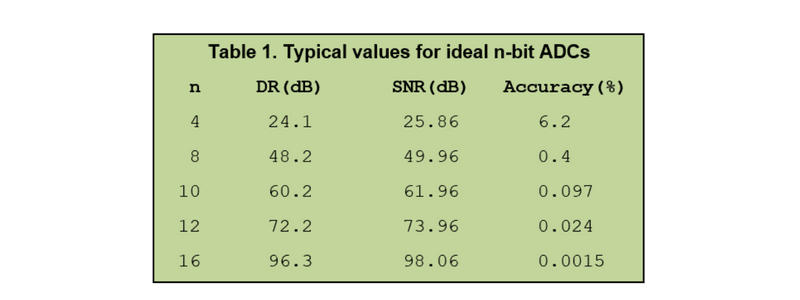
Ce tableau fournit un guide de référence rapide pour certaines tailles d'ADC communes. Il est très tentant de choisir les résolutions supérieures, mais vous pouvez voir dans le tableau qu'un ADC 8 bits donne une précision d'échantillonnage meilleure que 0,5 %. C'est adapté à la plupart des applications. Gardez à l'esprit que si le signal analogique échantillonné est bruyant (c'est généralement le cas), alors les bits inférieurs significatifs de l'échantillon deviennent inutiles. Ainsi, un ADC 16 bits peut théoriquement résoudre un tout petit signal, mais si par exemple les 4 LSB sont submergés par le bruit, alors le résultat ne sera pas meilleur que celui obtenu à partir d'un ADC 12 bits.
Véritables ADC et temps de conversion
Le processus de conversion analogique-numérique peut être réalisé selon diverses méthodes et si vous consultez des fiches techniques, vous tomberez sur des termes tels que "Flash" et "Approximation successive". Ces termes sont généralement liés au temps nécessaire pour convertir un échantillon. Les calculs théoriques ci-dessus supposent que la conversion est idéale, c'est-à-dire instantanée avec tCONV = 0. Naturellement, des composants pratiques prennent un temps fini de conversion au cours duquel l'entrée peut changer, c'est encore un autre facteur à prendre en compte lors de la conception. Il peut causer de graves inexactitudes si la fréquence d'échantillonnage est proche de la limite de Nyquist et que tCONV représente une proportion significative de la période d'échantillonnage. Il se peut que vous ayez besoin d'un dispositif appelé un Sample & Hold pour atteindre les performances requises. Heureusement, les DSP/microcontrôleurs modernes ont généralement cette fonctionnalité intégrée.
Processus inverse avec le CNA et reconstruction
Pour rappel, le convertisseur analogique-numérique (ADC) a échantillonné le signal d'entrée à une fréquence plus de deux fois supérieure à la composante de fréquence maximale présente dans ce signal. Ces échantillons, convertis en chiffres numériques, sont traités par un ordinateur qui exécute un algorithme qui réalise une certaine fonction comme un filtre passe-bas. La série d'échantillons de sortie de cet algorithme doit maintenant être reconvertie en une forme d'onde analogique.
Convertisseur numérique-analogique (CNA)
Les CNA de base sont beaucoup plus simples que des CAN. En fait, vous pouvez fabriquer vos propres CNA avec simplement une poignée de résistances et un amplificateur opérationnel ! Étrangement, alors que la plupart des microcontrôleurs sont chargés de canaux CAN, très peu sont dotés de la capacité de conversion numérique-analogique. Bien que vous puissiez fabriquer votre propre CNA , une bien meilleure idée est d'utiliser une puce CNA prête à l'emploi. Les CNA à usage général ne sont pas très chers, et à moins que vous ne recherchiez des vitesses très élevées (fréquence d'échantillonnage) et une haute résolution (nombre de bits), alors la monotonicité (la sortie augmente toujours avec chaque entrée numérique croissante) et la linéarité (des entrées numériques incrémentielles fournissent des tensions de sortie égales) peuvent être assumées.
Critères de sélection d'un CNA
La résolution et la plage dynamique du signal de sortie sont basées sur le nombre de bits numériques tout comme un CAN. Dans la plupart des cas, la résolution du CNA sera la même que celle de le CAN utilisé. En effet, il n'y a aucun intérêt à ce que le CNA ait une résolution plus élevée.
La fréquence d'échantillonnage doit également correspondre à celle de le CAN, mais très souvent, on trouve que la fiche technique présente la capacité de vitesse du CNA en exprimant son temps de stabilisation. Il s'agit du temps qu'il faut pour que la sortie analogique descende en dessous de ½ LSB de sa valeur finale lorsque l'entrée est comprise entre les valeurs minimale et maximale en une seule étape. Si on utilise un CNA 8 bits, par exemple, c'est le temps que prend la sortie pleine échelle pour se stabiliser une fois que l'entrée numérique est passée de 00 à FFh (pire des cas). Ce temps de stabilisation existe parce que :
- Les entrées numériques ne changent pas simultanément, donc pendant un bref intervalle, le CNA "voit" toute une variété de codes d'entrée.
- L'amplificateur de sortie a une vitesse de balayage finie et il faut du temps, après la stabilisation de l'entrée, pour que la sortie s'ajuste à la valeur correcte.
- Une capacité vagabonde peut provoquer le dépassement et le "bourdonnement" de la sortie.
Au cours du temps de stabilisation, un "signal transitoire" ou un "bourdonnement" s'affiche à chaque étape de tension de la sortie non filtrée. Ce n'est habituellement pas un problème tant qu'il ne dure qu'environ 10 % ou moins de la période d'échantillonnage. Le filtre passe-bas de reconstruction devrait le supprimer.
Le CNA parfait
Vous vous souvenez du "CAN parfait" de la dernière fois ? En théorie, il avait un intervalle d'échantillonnage de 0 et à ce titre pouvait avoir une fréquence d'échantillonnage infinie et n'avait pas besoin d'un filtre anticrénelage. Malheureusement, des composants pratiques ont un temps de conversion défini ce qui signifie que les fréquences d'échantillonnage sont définies et la largeur de bande de signal qui peut être échantillonnée est limitée. La Fig.1a et la Fig.1b illustrent la sortie idéale d'un CNA pour le domaine temporel et fréquentiel respectivement. Le signal numérique est une onde sinusoïdale unique. Notez que la sortie contient les mêmes composantes de fréquence que l'entrée échantillonnée d'origine. Le problème est qu'aucun CNA réel ne peut fournir des impulsions de largeur nulle, et des impulsions de largeur finie déforment le signal.
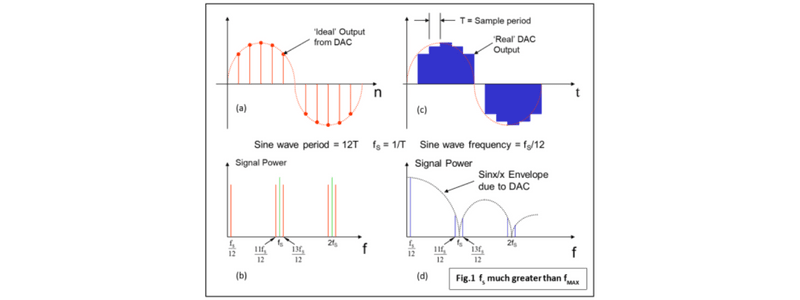
CNA réels et distorsion sinx/x
La Fig.1c et la Fig.1d montrent la sortie réelle d'un CNA typique et la distorsion de fréquence qui en résulte. Vous pouvez voir qu'un échantillon de sortie est constant pour l'ensemble de l'intervalle d'échantillonnage T. Il s'agit de la réalisation matérielle la plus simple : un CNA en entrée parallèle connecté à des broches GPIO verrouillées sur un microcontrôleur/DSP. La forme d'onde bleue a l'air très "ramassée" mais elle peut être nettoyée assez facilement avec un filtre passe-bas analogique ou de "reconstruction" parce que la fréquence d'échantillonnage est égale à douze fois la fréquence du signal. Les composantes de fréquence présentes dans le signal non filtré sont montrées dans la Fig.1d. Comme les échantillons de sortie sont de la même largeur que la période d'échantillonnage T, les composantes de fréquence sont atténuées par un sinx/x (prononcé "sinus x sur x"), avec la fréquence d'échantillonnage et ses harmoniques qui disparaissent complètement. La fréquence d'échantillonnage élevée signifie que la seule composante de fréquence que nous voulons dans la sortie finale (fS/12), l'onde sinusoïdale d'origine, est à peine touchée. Tout le reste serait supprimé par un filtre de reconstruction de toute façon.
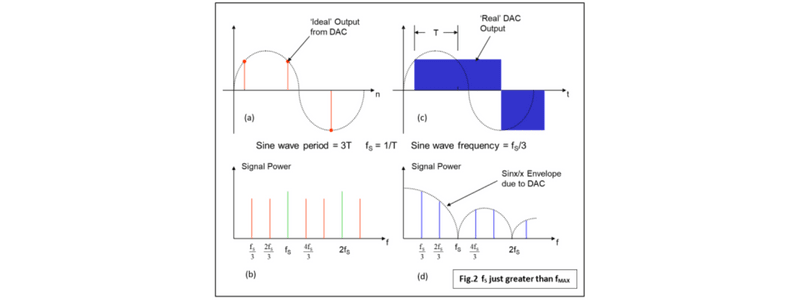
Par souci d'exhaustivité, nous allons examiner le même graphique pour un signal sinusoïdal de fréquence fS/3, tout juste supérieur à la limite de Nyquist fS/2 (Fig.2, ci-dessous). La sortie CNA a l'air encore plus "ramassée" mais le signal d'origine peut encore être récupéré car aucun crénelage ne s'est produit. Dans la Fig.2d vous pouvez voir que l'enveloppe sinx/x imposée a atténué notre composante de fréquence voulue fS/3 plus qu'avant et la fréquence non voulue 2fS/3 suivante est beaucoup plus proche et plus grande. Imaginez maintenant que fS/3 est simplement la plus élevée des composantes dans une bande de base de fréquences. Voyez comment la distorsion sinx/x introduit une coupure courbée significative sur la bande de base.
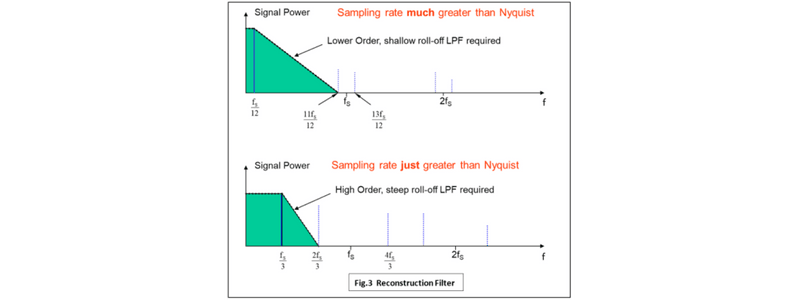
Reconstruction
Les filtres anticrénelages et de reconstruction sont des filtres passe-bas et effectuent des tâches similaires de suppression de composantes de haute fréquence non voulues. La bande anticrénelage limite le signal de bande de base prêt pour l'échantillonnage, la reconstruction supprime les fréquences indésirables résultant du processus d'échantillonnage en lui-même. Pas surprenant donc que les considérations de conception soient les mêmes pour les deux : une faible fréquence d'échantillonnage implique un filtre de coupure plus complexe et plus rapide. Une fréquence d'échantillonnage élevée permet d'utiliser une conception de coupure plus lente et plus simple.
Digital Signal Processing
Ainsi, nous avons désormais les moyens de convertir un signal analogique en une série de nombres qui peuvent être reconvertis en précisément la même forme d'onde par la suite. Ce n'est pas aussi inutile qu'il y paraît, car cela pourrait constituer la base d'un système de communication pour l'envoi de données analogiques sur un réseau numérique. La communication n'est pas le but ici : nous voulons traiter le signal dans sa forme numérisée. À peu près tout est possible, du filtrage simple à l'analyse spectrale en passant par l'extraction de caractéristiques depuis des images vidéo, le tout en temps réel.
Les outils essentiels pour une numérisation précise des signaux
En plus des avantages indéniables du traitement numérique du signal, il est crucial de prendre en compte les outils et composants essentiels pour garantir une numérisation efficace des signaux analogiques. L'utilisation de convertisseurs de signaux joue un rôle clé dans cette transition. Par exemple, des convertisseurs de signaux permettent de transformer des signaux de divers types en formats compatibles avec les systèmes numériques, facilitant ainsi la modélisation et l'analyse en temps réel. Pour en savoir plus sur les convertisseurs de signaux, vous pouvez consulter notresélection d'isolateurs et de convertisseurs de signaux sur notre site. Ces outils sont indispensables pour garantir que les signaux numérisés soient traités avec une précision optimale, tout en réduisant les erreurs liées à des facteurs tels que le coefficient de conversion ou les interférences.
Pour plus d'informations et de solutions adaptées à vos besoins spécifiques, visitez également notre page dédiée auxrelais et convertisseurs de signaux qui propose une large gamme de produits.
Éléments associés
Carte complément MC
Découvrez toutes nos cartes compléments MCU, avec un large choix pour répondre à vos besoins et vos prérequis.
Kit de développement
Tous nos kits de développement MCU pour vous permettre d'avancer dans vos différents projets.
Gants de sécurité
La protection des mains ne doit pas être prise à la légère, il faut choisir les gants adaptés contre le bon danger pour réduire tout risques.
Protection auditive
Dans les environnements bruyants, il est nécessaire de proposer une protection auditive adaptée, que ce soit un casque ou des bouchons.
Pour aller plus loin
Liens connexes
- Guide sur les signaux process : courant vs tension
- Carte complément MikroElektronika Volume 2 Click Traitement du signal pour Prise mikroBUS pour NJU72341
- Traitement thermique des aliments dans le secteur agroalimentaire
- Signal visuel clignotant à LED Clifford & Snell Jaune FD40
- Traitements de l'eau
- DSP (Digital Signal Processors)
- Conditionneur de signal
- Traitement de l'eau RS PRO 1.08L/s






